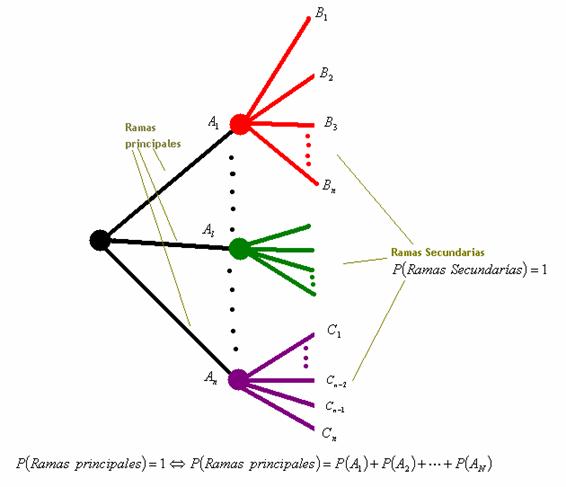
¿Qué es un diagrama de árbol?

Es una representación gráfica que inicia en una "raíz" de la cual se extienden las "ramas" que muestran cada uno de los resultados posibles de un experimento.

¿Cómo se construye?

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. Cada una de estas ramas se conoce como rama de primera generación

En el final de cada rama de primera generación se constituye a su vez, un nudo del cual parten nuevas ramas conocidas como ramas de segunda generación, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Ejemplos:

⦁ Un médico general clasifica a sus pacientes de acuerdo a: su sexo (masculino o femenino), tipo de sangre (A, B, AB u O) y en cuanto a la presión sanguínea (Normal, Alta o Baja). Mediante un diagrama de árbol diga en cuantas clasificaciones pueden estar los pacientes de este médico?

Si contamos todas las ramas terminales, nos damos cuenta que el número de clasificaciones son 2 x 4 x 3 = 24.

Las combinaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:

⦁ No influye el orden en que se colocan.

⦁ Si permitimos que se repitan los elementos, podemos hacerlo hasta tantas veces como elementos tenga la agrupación. Su fórmula es:

                                n!/r!(n-r)!

ejemplo:

¿De cuántas formas pueden mezclarse los siete colores del arco iris tomándolos de tres en tres?

solucion:

solo hay que sustituir la formula con los datos proporcionados: n=7      r=3

7!/3!(7-3)! = 35 formas

Permutaciones:

Las permutaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:

⦁ Influye el orden en que se colocan.

existen dos tipos de permutaciones: permutación con repetición y permutación sin repetición.

⦁ Serán permutaciones sin repetición cuando todos los elementos de que disponemos son distintos. Su fórmula es:  nr

ejemplo:

en una cerradura hay 10 numeros para elegir (0,1,,,,,9) y eliges 3 de ellos

solución:  vamos a utilizar la formula donde n va a ser los diez numeros y r va ser el exponente al que se va a elevar en este cas sera 3 = 10x10x10= 1000 permutaciones.

n!/(n-r)!

ejemplo:

¿cuantas cantidades de 3 cifras se pueden formar con los digitos 0,1,2,3y 4 si no se permite la repetición?

solución:

vamos a utiliar la formula de permutación sin repetición en este caso n= 5 y r=3

      5!/(5-3)! = 60 

Eventos mutuamente excluyentes

Dos o más eventos son mutuamente excluyentes o disjuntos, si no pueden ocurrir simultáneamente. Es decir, la ocurrencia de un evento impide automáticamente la ocurrencia del otro evento (o eventos). Para obtener la probabilidad de este tipo de evento se utiliza la REGLA ESPECIAL DE LA ADICION DE PROBABILIDADES, que es:

P (A o B) = P(A) + P(B)

ejemplos:

Si se tira un dado calcular la probabilidad de:

⦁ A: Caen 3 puntos o menos

⦁ B: Caen 5 puntos o más

P (A o B) = P(A) + P(B)

P (A o B) =P(salen 3 o menos) +P (salen 5 o más)

P (A o B) =3/6 + 2/6

P (A o B) =5/6 = 83.33%

Eventos mutuamente no excluyentes

Dos o más eventos son mutuamente no excluyentes si son sucesos que pueden presentarse simultáneamente. Para obtener la probabilidad de este tipo de evento se utiliza la REGLA GENERAL DE LA ADICION DE PROBABILIDADES, que es:

P (A o B) = P(A) + P(B) - P(A y B)

ejemplos:

Se elige al azar un número entero positivo del 1 al 19, ¿cuál es la probabilidad de que el número sea múltiplo de 3 o de 5?

⦁ A: 3, 6, 9 ,12, 15, 18

⦁ B: 5, 10, 15

⦁ A y B: 15

P (A o B) = P(A) + P(B) - P(A y B)

P (A o B) = 6/19 + 3/19 - 1/19

P (A o B) = 8/ 19 = 42%

Eventos Independientes

Dos o más eventos son independientes cuando la ocurrencia o no ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Para obtener la probabilidad de este tipo de evento se utiliza la REGLA ESPECIAL DE LA MULTIPLICACION DE PROBABILIDADES, que es:

P (A y B) = P(A) * P(B)

ejemplos:

En la urna A tenemos 7 bolas blancas y 13 negras y en la urna B 12 blancas y 8 negras. ¿Cuál es la probabilidad de que se extraiga una bola blanca de cada una?

P (A y B) = P(A) * P(B)

P (A y B) =7/20 * 12/20

P (A y B) =21/100 = 21%

Eventos dependientes

Dos o más eventos serán dependientes cuando la ocurrencia o no ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (u otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. Para obtener la probabilidad de este tipo de evento se utiliza la REGLA GENERAL DE LA MULTIPLICACION, que es:

P (A y B) = P(A) * P(B/A)

P(B/A): Indica la probabilidad de que ocurra un evento B si se sabe que ya ocurrió el evento A

P (B y A) = P(B) * P(A/B)

P(A/B): Indica la probabilidad de que ocurra un evento A si se sabe que ya ocurrió el evento B

ejemplos:

Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica se saca de la caja y no es remplazada. Otra canica se saca de la caja. ¿Cuál es la probabilidad de que la primera canica sea azul y la segunda canica sea verde?

⦁ A: Azul

⦁ B: Verde

P (A y B) = P(A) * P(B/A)

P (A y B) = 2/9 * 3/8

P (A y B) = 1/12 = 8.33%